Ontwerp vanfotonischegeïntegreerde schakeling
Fotonische geïntegreerde schakelingen(PIC) worden vaak ontworpen met behulp van wiskundige scripts vanwege het belang van de padlengte in interferometers of andere toepassingen die gevoelig zijn voor de padlengte.PICEen fotomasker wordt vervaardigd door meerdere lagen (doorgaans 10 tot 30) op een wafer aan te brengen, die bestaan uit vele veelhoekige vormen, vaak weergegeven in het GDSII-formaat. Voordat het bestand naar de fotomaskerfabrikant wordt gestuurd, is het zeer wenselijk om het fotomasker te kunnen simuleren om de correctheid van het ontwerp te verifiëren. De simulatie is onderverdeeld in meerdere niveaus: het laagste niveau is de driedimensionale elektromagnetische (EM) simulatie, waarbij de simulatie wordt uitgevoerd op subgolflengteniveau, hoewel de interacties tussen atomen in het materiaal op macroscopische schaal worden behandeld. Typische methoden zijn onder andere driedimensionale eindige-differentie-tijdsdomein (3D FDTD) en eigenmodus-expansie (EME). Deze methoden zijn het meest nauwkeurig, maar zijn onpraktisch voor de volledige simulatietijd van het fotomasker. Het volgende niveau is 2,5-dimensionale EM-simulatie, zoals eindige-differentie-bundelvoortplanting (FD-BPM). Deze methoden zijn veel sneller, maar leveren in op nauwkeurigheid en kunnen alleen paraxiale voortplanting simuleren en kunnen bijvoorbeeld niet worden gebruikt om resonatoren te simuleren. Het volgende niveau is 2D EM-simulatie, zoals 2D FDTD en 2D BPM. Deze zijn ook sneller, maar hebben een beperkte functionaliteit, bijvoorbeeld omdat ze geen polarisatierotatoren kunnen simuleren. Een verder niveau is transmissie- en/of verstrooiingsmatrixsimulatie. Elk belangrijk component wordt gereduceerd tot een component met ingang en uitgang, en de aangesloten golfgeleider wordt gereduceerd tot een faseverschuivings- en dempingselement. Deze simulaties zijn extreem snel. Het uitgangssignaal wordt verkregen door de transmissiematrix te vermenigvuldigen met het ingangssignaal. De verstrooiingsmatrix (waarvan de elementen S-parameters worden genoemd) vermenigvuldigt de ingangs- en uitgangssignalen aan de ene kant om de ingangs- en uitgangssignalen aan de andere kant van het component te vinden. In principe bevat de verstrooiingsmatrix de reflectie binnen het element. De verstrooiingsmatrix is meestal tweemaal zo groot als de transmissiematrix in elke dimensie. Samenvattend, van 3D EM tot transmissie-/verstrooiingsmatrixsimulatie, biedt elke simulatielaag een afweging tussen snelheid en nauwkeurigheid, en ontwerpers kiezen het juiste simulatieniveau voor hun specifieke behoeften om het ontwerpvalidatieproces te optimaliseren.
Het gebruik van elektromagnetische simulatie van bepaalde elementen en een verstrooiings-/overdrachtsmatrix om de gehele PIC te simuleren, garandeert echter geen volledig correct ontwerp vóór de stroomplaat. Foutief berekende padlengtes, multimode golfgeleiders die er niet in slagen hogere-orde modi effectief te onderdrukken, of twee golfgeleiders die te dicht bij elkaar liggen en daardoor onverwachte koppelingsproblemen veroorzaken, kunnen bijvoorbeeld onopgemerkt blijven tijdens de simulatie. Hoewel geavanceerde simulatietools krachtige mogelijkheden bieden voor ontwerpvalidatie, vereist het daarom nog steeds een hoge mate van alertheid en zorgvuldige inspectie door de ontwerper, in combinatie met praktische ervaring en technische kennis, om de nauwkeurigheid en betrouwbaarheid van het ontwerp te waarborgen en het risico op fouten in de stroomplaat te minimaliseren.
Een techniek genaamd sparse FDTD maakt het mogelijk om 3D- en 2D-FDTD-simulaties rechtstreeks uit te voeren op een compleet PIC-ontwerp om het ontwerp te valideren. Hoewel het voor elk elektromagnetisch simulatieprogramma moeilijk is om een zeer groot PIC te simuleren, kan sparse FDTD een relatief groot lokaal gebied simuleren. Bij traditionele 3D FDTD begint de simulatie met het initialiseren van de zes componenten van het elektromagnetische veld binnen een specifiek gekwantiseerd volume. Naarmate de tijd verstrijkt, wordt de nieuwe veldcomponent in het volume berekend, enzovoort. Elke stap vereist veel berekeningen, waardoor het lang duurt. Bij sparse 3D FDTD wordt, in plaats van bij elke stap op elk punt van het volume te berekenen, een lijst met veldcomponenten bijgehouden die theoretisch kan overeenkomen met een willekeurig groot volume en alleen voor die componenten wordt berekend. Bij elke tijdstap worden punten die grenzen aan veldcomponenten toegevoegd, terwijl veldcomponenten onder een bepaalde vermogensdrempel worden verwijderd. Voor sommige structuren kan deze berekening vele malen sneller zijn dan traditionele 3D FDTD. Sparse FDTDS presteren echter niet goed bij het omgaan met dispersieve structuren, omdat het tijdsveld zich te veel verspreidt, wat resulteert in te lange en moeilijk te beheren lijsten. Figuur 1 toont een voorbeeldschermafbeelding van een 3D FDTD-simulatie die vergelijkbaar is met een polarisatiebundelsplitser (PBS).
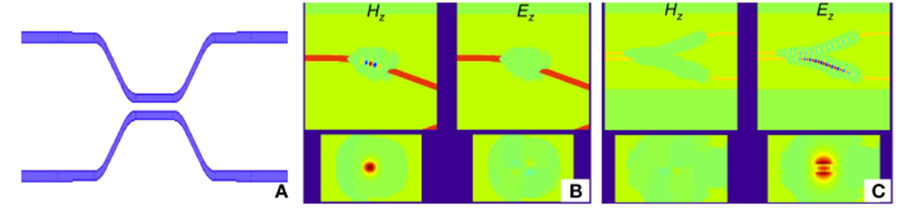
Figuur 1: Simulatieresultaten van 3D sparse FDTD. (A) is een bovenaanzicht van de gesimuleerde structuur, een directionele koppelaar. (B) Toont een screenshot van een simulatie met quasi-TE-excitatie. De twee diagrammen hierboven tonen het bovenaanzicht van de quasi-TE- en quasi-TM-signalen, en de twee diagrammen hieronder tonen de corresponderende dwarsdoorsnede. (C) Toont een screenshot van een simulatie met quasi-TM-excitatie.
Geplaatst op: 23 juli 2024





